ミノ駆動本を読みました

本の紹介

gihyo.jp

これです。最近何かと話題になっているのをみたのと、競プロライブラリの構成に迷ってたので、何か解決しないかなと読んでみました。

自分にとっての感想

自分視点だと学ぶことが余りなかったように感じました。というのも、内容が嫌いというよりは、これまでライブラリ整備をしてきた中で直面して調べた問題や他の人のライブラリを見る中で学んだことのまとめという感じでした。いい復習にはなるし、これまで悩んでたことって割といい問題だったんだなとも思えたので読むのは楽しかったです（1日かけて読了）。

ライブラリ整備を始めてみたい！みたいな方にはおすすめできます。こだわりが強くなって精進をする人から盆栽をする人にジョブチェンジしてしまう可能性もあるので、そこは自己責任。

1年前から業プロを始めたのですが、憧れている先輩のコードが確かにこうなっているなあと思える場面が多かったです。

でも難しいですね。バカでかclassを使わざるを得ない時や、計算量的にvecのcloneを毎回するべきではない時があります。個人的にはトレードオフの関係だと思っています。 満たすべき要件を整理した上で、自分がbetterだと思える選択をしたい（これが難しい）。

こういう内容を全員が知っておくべきとは言わないんですが、開発しやすい変数ってどんなかな~とか、変更範囲をどこにまとめようかな~とかみんなが考えることができると、嬉しいですね。みんなが考えて議論していけば、変更しやすいコードになっていく気がする。とはいえ、業務で書くコードって合計10000行とかになってしまうので、ある程度は慣れるまで時間がかかってしまいます。なんか半年かけてやっとコード全体像がわかってきたってレベルです。ドメイン知識が難しいので、仕方ないのかな。

Rust

あとRustが素晴らしいですね。mut や &mut、 & で所有権や可変性などについて教えてくれているので、安心できます。なんかこういうのが怪しい分野があるらしい（unsafeな世界）ので、挑戦するときは気をつけたい。

あと trait の使い方が見えた気がしました。traitの関数に初期設定（特にオーバーロードしなかったらこうなる）みたいなのができて、実際に使用するクラスでオーバーライドするか選べるみたいな機能があると嬉しい気がしていたけど、機能の異なる関数を同じロジックで流用する気もしてきた。迷うぜ、、、。

Python

Pythonが僕が普段使っているオブジェクト指向言語なんですが、これには活かせる場面が多そうですね。それはそうと早くPythonにはクラス変数にprivate, public 設定をください。_とかいうローカルルールを許すな！！

宣伝

github.com

私の競プロライブラリです。使ってみてね。

蟻本初級を読み終わりました

世の中のほとんどの人は本を読み切ることができません。今回私は、蟻本の初級編をなんとか読み終えることに成功しました。 そこで、その感想をブログにしてみました。

蟻本とは

https://book.mynavi.jp/ec/products/detail/id=22672

です。

元々の実力

水色下位です。得意はなくて、ABCを下から埋めるだけをしていました。パフォーマンスは800~1800くらいで安定感ないです。

かかった時間

わかりません。その時の気分によって、2日くらい悩んでみたりすぐに答えを見たり（よくない）してるので。。。

Rustの解答

github.com

間違えているところあったら教えてくれると嬉しいです。

問題への感想

それぞれの問題に対して、思ったことを書いていきます。

2-1

全探索は基本ですね。問題を見た時に全探索をすると計算量がアホだから改善をしなきゃ見たいな視点を忘れたくない。

部分和問題

bit全探索ですね。典型です。半分全列挙とかで早くなる見た目をしています。

Lake Counting

意外とこういうの苦手なんですよね。

for i in 0..w {
    for j in 0..h {
        if !flag[i][j] {
            dfs をする
        }
    }
}

みたいな典型です。グリッド全てに対して、dfsを何回できるかをこのようにかくの賢いと思いました。

迷路の最短路

bfsならキューの中が広義単調増加になるので、最短路がわかるやつですね。 冷静になると、これがデータ構造の中身にいい性質があるのでできるやつの一例ですね。（LISとかstackで頑張るやつみたいな） グリッドの操作を、[(1, 0), (0, 1), (!0, 0), (0, !0)] に対して、 wrapping_add() でやると楽ですね。

2-2

貪欲のアルゴリズムは例をちゃんと見てみると思いつくものが多くて時間がかかります。あ、頭が悪いだけでした。

硬貨の問題

これって、硬貨1枚の値段が変な設定だったら貪欲が成り立たないですね、、、と思ってました。本当ですか。 日常でよく考えているので簡単に思いつきますね。

区間スケジューリング問題

できるやつでなるべく早く終わるものから取り掛かりたいってやつでよく見ますね。 仕事でこれをしたいんですが、できない仕事の存在が許せないのでアレです。

Best Cow Line

これ、すごく回りくどい解き方（逆順を比較するのではなく、一文字ずつ後ろにずらして比較（結局同じこと））をしてしまいました。文字列の順序の付け方から先頭になるべく良いものを持ってきたいっていうので解けますね。同じ文字の時にどうするかを結構迷って、次の文字を比較かってなれて嬉しかったです。

Saruman's Army

こういう問題、実装をちゃんと考えないと面倒くなりがち（個人の感想）。

Fence Repair

これ面白いですね。例を見ていると小さなものから合成する貪欲は思いつくんですが、木を構築すると証明ができるのすごいと思いました。

2-3

DPは式から先か、DPで解けそうという嗅覚が先か。

全部漸化式を立ててから解いてます。

01ナップサック問題

これをDPで解こうという理由がわかりました。DPってメモ再帰の一例なんですね（本当か？）。

最長共通部分列問題

これはどうしてDPで解くんですか？？ってなっています。こういう2次元DPが苦手なんですけど言語化が下手で困ります。 前から見ていくという方針を取ろう！って思う理由がわかってないです。 ちなみにDPという先バレがあったので、解けました。GOGOランプが光ってました。

個数制限なしナップサック問題

こういう遷移の個数を減らす問題ですが、式変形を上手にするよりも遷移のグラフを考えた方がわかりやすいです。

01ナップサック問題その2

典型ですね。

個数制限付き部分和問題

これ解けませんでした。確かにDPテーブルにbool値を持つよりも上手い情報の載せ方あるなあと思いました。 こういうのは「余る」よりも「使う」にした方がわかりやすくて好きです。賢い方法ですね。

最長増加部分列問題

これは典型ですね。知っていました。 $O(n \log n)$ でオーバーキルします。

分割数

これも解けませんでした。 $i$ の $j$ 分割数みたいなDPを立てるのができませんでした。なんならDPの遷移式も思いつきませんでした。組み合わせで殴れないか考えていました。

重複組合せ

漸化式で差をとると簡単な形になります。これはかなり考えて解けました。 ここら辺のDPは難しく感じます。少なくとも緑diff以上はアリそう。

2-4

データ構造です。全て作成済みなので使い方を学んでいくう。

Expedition

止まるたびに一番多く入れれたところで入れたことにすればいいやつですね。2-2をクリアした私にとってこの程度の貪欲、舐めないでいただきたい。

Fence Repair

もうすでにしばいていました。

食物連鎖

これとても難しいですね。2日間くらいずっと悩んでました。 最終的には解けたんですが、xがAかBかCかを後で決めたいんだよなあ、、、、となった末に、同時に起こるべきものを結んでいくという案に辿り着きました。

この問題を解いたすぐ後に食物連鎖に関するツイートが回ってきて、爆笑していました。

二部グラフ判定

これはLake Countingみたいにdfsを続ければ良い問題ですね。2-1を学んだ私にとってこの程度、、、ふぅ。。

Roadblocks

なんか解けてしまったやつです。ダイクストラを二番目までやればいいのはそれはそうなんですが、計算量解析が、、、。

Conscription

Lake Countingの如く、森それぞれに対してMSTをしました。

Layout

牛ゲー（うしゲーなのかぎゅうゲーなのか）。これは解けませんでした。答えを見た結果、わけがわからずとりあえず数理最適化問題としてちゃんと定式化を理解しました。（双対問題はそういうものだと理解しただけ。。） Twitterに聞いてみたところ、こめだわらさんが助言をくれて理解が進みました。 まだ、考えている最中なところでもある感じなのでまとまったら、いつかブログを書きます。

2-6

線分上の格子点の個数

すぐに解けましたが、例外処理を忘れていました。あーあ。

双六

ユーグリットの互助法の復元のやつですね。毎回、再帰で書いていたんですが、ちゃんとライブラリ化しました。

素数判定

もちろんミラーラビン。

素数の個数

エラトステネスの篩を書きました。線形篩なるものもあるっぽいですね。ここら辺は簡単です。計算量解析も証明は無理ですが、有名事実として使って仕舞えば怖くない。

区間内の素数の個数

これ正規の方法では解けませんでした。しかし、ミラーラビンで十分殴れてしまいました。 正規の方法の方は確かになんですが、難しかったです。エラトステネスの篩の原理にちゃんと立ち返れなかったの反省です。

Carmichael numbers

ミラーラビンで嘘をついてくるやつですね。pow modを愚直に計算しても間に合うので余裕でした。より高速な解法は考えてもわかっていません。人生の課題です。

2-7

Minimum Sclar Product

$n = 2$ の場合での貪欲がわかったことから、全体にも派生できました。こういう小さな場合で考えるの大事ですね。例示は理解の試金石です。（数学ガールより）

Crazy Rows

これは上の列になればなるほど条件が厳しいことから貪欲が思いつきました。もちろん $O(n²)$ で書きました。

Bribe the Prisoners

これは区間再帰であることに気づけました。（問題ではDPみたいですね。DPで解こうとはならないかも） この問題を見ている時くらいから、DPは再帰の特別な場合なので、別にそこまで意識せずにDPの形の方が実装しやすい時にそうすれば良いなくらいのメンタルになりました。

Millionaire

最後の問題なのに解けませんでした。連続的だしいい貪欲あるんだろうな（小並感）の元に考えましたが、無理でした。 回答を見たんですが、最後の1ケースから巻き戻して考えるのいいですね。次出てきた時に解ける気がしていないので、もう少し考えたい。。

学んだこと

蟻本難しい。考え方のヒントみたいなのがたくさん散らばっている問題が多い気がしました。 考察が詰まった時に、どう考えていくのがいいのかな？みたいなのが色々あって定期的に思い出す and しっかり身につける をしたいです。 中級編も楽しみ〜〜

2024年まとめ

お疲れ様です。

自分のレート変化

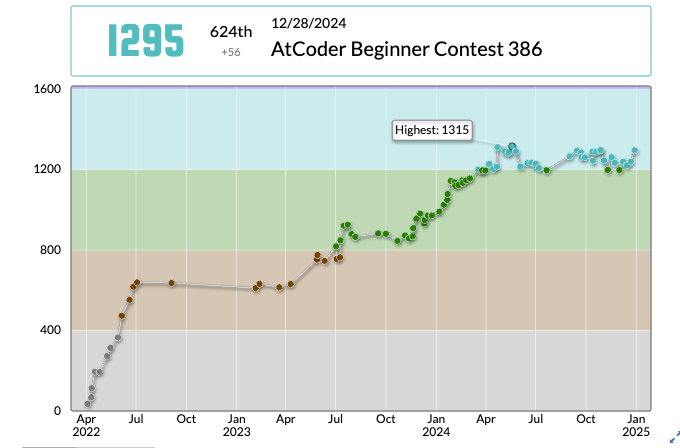
2024年の間で、984から1295まで増加しました。成長は嬉しいね。

できるようにならなかったこと

2次元DPが降ってくること

例えば、 の 分割数を求める際にDPをしようみたいな発想ができません。 の関数として捉えて式変形をするようにすれば、 の の分割数が全て求めることができればこれも求めることができると考えることはできます。

DPを思いつく過程としてはこっちの方が正しいのかなという感覚もありますが、AtCoderの解答にはDPを思いつくのが第一みたいな書き方が多いので、周りくどい考え方をしていそうだなとも思ってしまいます。

得意分野を作ること

チーム戦をする時などは特に感じてしまいます。数学専攻だったのでこれを活かしていきたいとは思っていましたが、別に数学問題が得意なわけではないので苦しいです。

普段の精進方法が「ABCの過去回を前から解く」だったので、まあ得意分野なんてできるわけがない気もします。

水perfを安定させること

時々、茶や緑perfみたいな回があります。

自分の知らないアルゴリズムやデータ構造がある気がしてC, D問題くらいでネット徘徊をしている時とかにこれになりがちです。 一旦落ち着いて今の手持ちでできることがないかを考えるようにしたいですが、一度楽できる気がするとそっちに頭が向いてしまう。。。。ああああああ。

あとはstackやdequeを上手に使う問題が苦手かもしれません。stackやdequeの内部である良い性質が常に成り立つことを利用する問題とかで、その性質を忘れがちです。ちゃんとコメントアウトで書いておくことを徹底しています。

できるようになったこと

Rust のコードを美しく書く

Rustの既に用意されている関数や、イテレータの使い方が徐々に身についてきました。提出コードにちょっと自信があります。とくとご覧あれ。

自然な発想を追い求めること

典型問題と分類するのは嫌いです。解法をどういう思考のプロセスで導くことができるかを考えています。なるべく発想に乖離がないようにしたいのですが、ここら辺は難しいです。高校数学みたいな楽しさがあります。

最近は「例示をすることで良い性質を見つけにいく」という技を身につけました。数学ガールでも似たようなのありましたね。

来年にしたいこと

色々な典型を学ぶこと

自然な発想もいいのですが、先人の知識も素晴らしいものです。平方分割や主客転倒など名前は知っているが、中身を知らないものがたくさんあります。 蟻本を買ったので、読み進める中で典型問題を学んでいきたいと思います。

得意分野を作ること

形式的冪級数や数え上げ、グラフ、グリッド、構築、幾何、数学など分野ごとに集中的に学ぶ期間を作って、自分が得意な分野を探していきたいです。

Haskellで競プロをすること

黄色以上になってABCがアンレになった後のことを考えています。気が早くね。

友達を作ること

仲の良い人と一緒に考察や感想戦をすることの楽しさをチーム戦で知ってしまいました。Xの返信とかをめんどくさくてサボりがちですが、皆さんのことは大好きです。一緒に成長しましょう。

まとめ

ここまで読んでいただいてありがとうございました。来年も仲良くしていただけると嬉しいです。